[Next][Up][Previous]
Next:KonklusionUp:Das Menschliche Gehirn -Previous:Einführung

Subsections

Wie unterscheidet sich ein künstliches Neuronales Netz von seinem Vorbild in der Natur?

Vorboten eines neuen Typs intelligenter Rechner

Die Entwicklung von Rechnern, die gemäß dem im ersten Abschnitt vorgestellten alternativen Intelligenz-Kriterium als intelligent zu bezeichnen wären, erfordert ein radikales Umdenken. Ich werde in diesem Abschnitt einige erfolgversprechende Ansätze skizzieren.

Vom Logiker zum Käfer: Wechselnde Vorbilder für Maschinelle Intelligenz

Lange Zeit war bei der Entwicklung maschineller Intelligenz das Hauptziel, einen maschinellen Theoretiker zu schaffen, also eine Maschine, die ein theoretisches Modell ihrer Umwelt aufbaut, und die zur Lösung eines konkreten Problems Strategien sucht für die sie logisch herleiten kann, daß sie optimal sind. Bei diesem Ansatz ist man auf zwei Probleme gestoßen:

$\bullet$: Solange der Rechner keine begleitende Intuition für sein theoretisches Welt-Modell besitzt, muß er bei der Berechnung von sachgerechten Problemlösungen mehr oder weniger blind suchen bis er zufällig auf eine Strategie stößt, die ``paßt''. Für ihn ist ja jede mögliche Strategie oder ``Aktion'' nur eine Zeichenreihe, die genauso gut in Chinesisch kodiert sein könnte, weil er ihren Inhalt sowieso nicht versteht. Da der Suchraum für mögliche Problemlösungen in der Regel exponentiell groß ist in der Komplexität n des Problems (wobei man n als die Anzahl der ``Freiheitsgrade'' oder Teilschritte von möglichen Strategien auffassen kann), führt dies schon bei relativ einfachen Problemen (also zum Beispiel für n=100) zu einer erforderlichen Anzahl von Rechenschritten der Größenordnung 2¹⁰⁰. Die allerschnellsten gegenwärtig existierenden Rechner können weniger als 2⁴⁴ Rechenschritte pro Sekunde ausführen. Zur Ausführung von 2¹⁰⁰ Rechenschritten würde solch ein Rechner 2⁵⁶ Sekunden, also ca. 1 000 000 000 Jahre benötigen.
$\bullet$: Ein weiteres und möglicherweise noch schwierigeres Problem ist das folgende: Wir als Menschen schaffen es in der Regel halbwegs richtige Entscheidungen im Alltagsleben zu treffen, obwohl sowohl das uns zur Verfügung stehende Hintergrundwissen^[Kommentar] als auch die unmittelbar für die Entscheidung relevanten Sinneseindrücke in der Regel vieldeutig und oft sogar widersprüchlich sind. Diese Komplikation wird uns meist gar nicht bewußt solange wir nicht darüber nachdenken. Sie führt aber zur bedauerlichen Tatsache, daß die Kalküle der mathematischen Logik und die bisher vorhandenen Methoden des maschinellen Beweisens nicht geeignet sind um einer Maschine in einer natürlichen Umgebung sachgerechte Aktionen vorzuschlagen.^[Kommentar]

Ein besonders interessantes Anwendungsgebiet für maschinelle Intelligenz ist die Robotik. Die beiden genannten Probleme haben bewirkt, daß ein mit traditioneller künstlicher Intelligenz, also mit Hintergrundwissen und logischen Schlußweisen, ausgestatteter autonomer mobiler Roboter sich in einer nicht speziell für ihn präparierten Umgebung in der Regel nur peinlich langsam und nicht besonders zufriedenstellend bewegt.

Ein überraschender Neuansatz zur Lösung dieses Problems, der heute oft als ``Neue Robotik'' bezeichnet wird, wurde der staunenden Fachwelt im Jahr 1986 von Rodney Brooks^[Link]vom MIT in Cambridge (USA) vorgestellt. Genaugenommen waren einige dieser revolutionären Ideen schon vorher von einem krassen ``Außenseiter'' in der Robotik, dem Neurophysiologen Valentino Braitenberg, vorgeschlagen worden.^[Link] Als Alternative zu den damals besten Robotern, die große Rechner mit sich herumschleppten und lange darüber ``nachdenken'' mußten wie sie einem Hindernis ausweichen sollten, stellte Rodney Brooks kleine käferartige Leicht-Roboter vor, die flink durch die Gegend wieselten und Hindernisse geschickt umgingen. Ihre Rechner-Architektur beruht auf einem neuen Prinzip, das technisch als Subsumptionsarchitektur^[Kommentar] bezeichnet wird. Hier versucht man nicht mehr, ein immer komplizierter werdendes Modell der Wirklichkeit im Rechner nachzubauen und bei Entscheidungen zu befragen. Stattdessen besteht das ``Innenleben'' dieser neuen Wesen aus einem geschickt koordinierten Bündel von spezialisierten ``Reflexen'', zum Beispiel dem Reflex ein unmittelbar vor ihm befindliches Hindernis zu umgehen, oder dem Reflex eine Ladestation aufzusuchen, sobald die Spannung am Akku des Roboters eine Schwelle unterschreitet, oder dem Reflex ein bestimmtes vom Benutzer vorgegebenes Ziel aufzusuchen. Das Prinzip von Brooks' Subsumptionsarchitektur besteht darin, daß zunächst jeder einzelne dieser Reflexe für sich möglichst direkt durch geeignete Verbindungen von den ``Sinnesorganen'' (d.h. von Lichtsensoren, sonaren Sensoren, Kameras oder Laser-Abstandsmessern) zu den Motoren des Roboters in möglichst einfacher und stabiler Weise implementiert wird (mehr dazu im nächsten Unterabschnitt). Für den Fall, daß verschiedene dieser Reflexe zu gegensätzlichen Motor-Kommandos führen, werden solche Konflikte intern in einer Weise gelöst, die das langfristige ``Überleben'' des Roboters optimiert. Zum Beispiel: wenn die Akku-Spannung niedrig ist, aber ein Hindernis auf dem direkten Weg zur Ladestation auftaucht, dann ist es momentan wichtiger diesem Hindernis auszuweichen als zu versuchen, mit ``dem Kopf durch die Wand'' auf dem direktesten Weg zur Ladestation zu gelangen.

Der geschilderte Neuansatz von Rodney Brooks ist aus der gegenwärtigen Robotik nicht mehr wegzudenken. In Schwierigkeiten gerät dieser Ansatz dort, wo die Vielfalt der zu kontrollierenden Reflexe oder die Kompliziertheit der zu bewältigenden Aufgaben es dem Ingenieur nicht mehr erlauben, die Regeln für ein geeignetes Zusammenspiel der Reflexe mittels seiner eigenen Intuition festzulegen. Ein menschlicher Betrachter dieser Problematik ist vielleicht erinnert an nicht ganz unähnliche Konflikte zwischen kurz- und langfristigen Zielen verschiedener Art, die sich - teilweise unbewußt - im Menschen abspielen.^[Link]

Ein gemäß der Subsumptionsarchitektur konstruierter Roboter ist zwar einem relativ ``primitiven'' Lebewesen wie einem Käfer sehr viel ähnlicher als einem komplexen Lebewesen, aber im Unterschied zu einem gemäß der traditionellen künstlichen Intelligenz konstruierten Roboter haben einige dieser Reflexe eine unmittelbar erfahrbare Bedeutung für ihn: die gegenwärtige Akkuspannung ist zum Beispiel nicht eine Zahl wie jede andere, sondern sie ist ein unmittelbarer Indikator dafür wie lange er noch umherfahren kann bevor er eine Ladestation aufsuchen muß. Ebenso ist ein hoher Meßwert von Infrarot-Sensoren in Fahrtrichtung ein recht sicheres Vorzeichen für eine unmittelbar bevorstehende Kollision. In diesem Sinn haben diese Sensor-Werte eine unmittelbare Bedeutung für den Roboter. Sobald aber intern kodierte Informationen eine direkte Bedeutung für die Existenz einer Maschine haben, erfordert es nur einen kleinen zusätzlichen Schritt, daß die Maschine Gefühle zeigt, also zum Beispiel Freude über eine Akku-Ladung oder Sorge, falls eines seiner Räder nicht mehr die gesendeten Dreh-Befehle ausführt (siehe zum Beispiel die ausführliche Diskussion in Kapitel 2 von [Picard, 1997]).

Zugegebenermaßen sind die angesprochenen praktischen Probleme, wie die Vermeidung von Kollisionen, recht primitiv, verglichen etwa mit den abstrakten Überlegungen eines Logikers oder Mathematikers. Vielleicht haben beide Bereiche aber trotzdem etwas miteinander zu tun: Hat nicht fast jeder Logiker und Mathematiker -- bewußt oder unbewußt -- räumliche Bilder vor Augen, selbst bei vollkommen abstrakten Gedankengängen, also auch beim formalen Denken? Ist dieser Effekt vielleicht ein Überbleibsel des ``Käfers in uns'', oder genauer gesagt: der über Millionen von Jahren der Evolution angesammelten Erfahrungen im Umgang mit 3-dimensionalen Objekten? Und liegen die zahlreichen Mißerfolge beim Versuch kreatives formales Denken (zum Beispiel: maschinelles Beweisen) von Rechnern durchführen zu lassen, vielleicht daran, daß man zu geradlinig versucht hat, den Rechner wirklich rein ``formal'', also ohne begleitende quasi-räumliche Anschauung, denken zu lassen -- was selbst uns Menschen kaum gelingt?

Schließlich möchte ich anmerken, daß der Paradigmenwechsel ``vom Logiker zum Käfer'' in der Robotik weniger perfekt ist als ich es bisher dargestellt habe. Probleme treten schon dann auf, wenn man in einem komplexen Roboter das Zusammenspiel seiner ``Reflexe'' so gestalten möchte, daß sein ``Überleben'' optimiert wird. Man ist versucht, dem Roboter hierfür Hintergrundwissen über die relative Wichtigkeit einzelner Reflexe einzuprogrammieren, aus denen er sich sinnvolle Koordinationsregeln logisch herleiten kann (zum Beispiel: ``Auch wenn die Akku-Spannung niedrig ist, müssen Hindernisse auf dem Weg zur Ladestation umgangen werden.'').

Bei Käfern und anderen Lebewesen ist das Zusammenspiel der Reflexe im Laufe der Evolution über Millionen von Jahren hinweg soweit optimiert worden, daß sie damit überleben können. Diese Methode hat man auch in der gegenwärtigen Robotik erfolgreich eingesetzt: Indem man eine ``Evolution'' künstlich simuliert, also Teilstücke der Reflex-Koordination der überlebensfähigsten Exemplare der gegenwärtigen Generation von Robotern in verschiedenen Weisen rekombiniert (``Kreuzung'') und lokal zufällig verändert (``Mutation''). Aus der so entstehenden neuen Generation von Robotern wählt man wiederum die überlebensfähigsten aus und iteriert dann das geschilderte Verfahren. Schöne Beispiele von Anwendungen dieser sogenannten ``genetischen Algorithmen'' in der Robotik werden zum Beispiel in den Arbeiten der Robotik-Gruppe der EPFL Lausanne geschildert.^[Links]

Der wesentliche Nachteil dieser Technik besteht darin, daß sie in der Praxis erfordert, die individuell Überlebensfähigkeit von Hunderten und Tausenden verschiedener Roboter-Varianten zu evaluieren. Das nimmt sehr viel Zeit in Anspruch. Daher ist es sinnvoll, diese Evolutionstechnik zu ergänzen durch schnellere Lernmethoden, die schrittweise die Überlebensfähigkeit eines einzelnen Roboter-Individuums verbessern können. Solche Techniken werden im nächsten Unterabschnitt skizziert.

Am Rande möchte ich anmerken, daß beide Techniken im Prinzip natürlich auch im Bereich nicht-mobiler Rechner anwendbar sind, also dort wo die ``Bedrohungen'' - abgesehen von einem Stromausfall - nicht physischer Natur sind, und wo ``überleben'' für einen Rechner bedeutet, möglichst lange eine hohe Rechenleistung ohne ``Absturz'' aufrecht zu erhalten.

Maschinen, die aus ihren eigenen Erfahrungen lernen

Ein wesentlicher Bestandteil des in unserer Gegenwartskultur verankerten Begriffs der Maschine ist die Vorstellung, daß das Verhalten einer Maschine insofern ``trivial'' ist, als sie nur das ausführen kann, was ihr von ihrem menschlichen Erbauer vorher einprogrammiert wurde. Diese Vorstellung ist veraltet, weil es in den Forschungslabors^[Links], in der Industrie, und sogar schon in der Unterhaltungselektronik^[Link] eine Reihe von Programmen gibt, die es Rechnern ermöglichen, aus ihrer eigenen Erfahrung zu lernen. Insbesondere können solche lerndenden Maschinen eine durch ihre vorhergehenden Erfahrungen geformte Individualität hervorbringen, die selbst von ihrem menschlichen Erbauer nicht vollkommen vorhersehbar ist. Das einzige, was der menschliche Erbauer einer solchen Maschine kennt, ist deren Lernalgorithmus, also das von ihm einprogrammierte Verfahren, mit dem die Maschine neue Verhaltensmuster aufgrund von vorhergehenden Erfahrungen entwickeln kann. Eine Vielfalt solcher Lernalgorithmen ist inzwischen bekannt [Weiss and Kulikowski, 1991,Mitchell, 1997]. Viele der in den Entwicklungslabors bisher erfolgreichsten Lernalgorithmen sind den Lernmechanismen von lebendigen Organismen abgeschaut worden.^[Kommentar] Als Beispiele erwähne ich das Reinforcement Lernen^[Kommentar] [Sutton and Barto, 1998], sowie das Lernen mittels künstlicher Neuronaler Netzwerke [Arbib, 1995]. Das Reinforcement Lernen ist von besonderem Interesse im Kontext des im ersten Abschnitt geschilderten alternativen Intelligenzkriteriums, weil es direkt auf dem Prinzip aufbaut, gegenwärtige Aktionen jeweil so zu wählen, daß die langfristige Belohnung (zum Beispiel: langes Überleben) maximiert wird. Ein weiterer interessanter Aspekt des Reinforcement Lernen ist die Tatsache, daß es dem Rechner, bzw. dem davon gesteuerten Roboter, beibringt, ständig abzuschätzen, wie weit er von einem vorgegebenen Arbeitsziel noch entfernt ist. Wenn man möchte, kann man das auf diese Weise erzielte Wissen der Maschine über ihre eigene Situation ^[Link] als rudimentäre Vorform eines maschinellen Bewußtseins bezeichnen.

Von der Biologie inspirierte neue Rechnerstrukturen

Die traditionelle Struktur unserer Rechner ist gekennzeichnet durch folgende Merkmale:

$\bullet$: Speicher und Rechnen sind getrennt
$\bullet$: der Rechner kann nur ausführen, was im Programm ``vorhergedacht'' wurde
$\bullet$: hierarchisch geordnet, sequentielle Arbeitsweise
$\bullet$: Rhythmus durch zentralen Taktgeber vorgegeben
$\bullet$: Kommunikation intern und extern mittels Bits
$\bullet$: Die Prozessoren bestehen aus Gattern, die eine geringe Zahl binärer Inputs verarbeiten.

Im Gegensatz dazu besitzt die Informationsverarbeitung in biologischen Nervensystemen die folgenden charakteristischen Strukturmerkmale:

$\bullet$: Speicher und Rechnen sind kombiniert in den informationsverarbeitenden Grundbausteinen (Neuronen und Synapsen)
$\bullet$: das Nervensystem kann aus Erfahrung lernen
$\bullet$: es ist überwiegend "demokratischßtrukturiert, d.h. es gibt keine zentrale Befehlsausgabe und die Neuronen und Synapsen arbeiten weitgehend autonom
$\bullet$: es gibt keinen zentralen Taktgeber, die zeitliche Abfolge der internen ``Rechenschritte'' hängt vom konkreten Input ab
$\bullet$: interne Kommunikation und Output mittels spike trains, also zeitlichen Mustern von Pulsen
$\bullet$: Neuronen erhalten durch direkte Verbindungen Signale von 5000 - 10000 anderen Neuronen.

In der Zwitterwelt zwischen diesen beiden Rechnerstrukturen sind die künstlichen Neuronalen Netze angesiedelt. Diese folgen in ihrer Architektur eher den Prinzipien biologischer Systeme, können aber in jedem üblichen digitalen Rechner simuliert, oder direkt in neuartiger elektronischer hardware implementiert werden.^[Kommentar]Ihre Merkmale sind die folgenden:

$\bullet$: Sie bestehen aus künstlichen Neuronen, die mittels geeigneter Computer-Programme oder sogar mittels dafür entwickelter neuer elektronischer Hardware in einem Computer simuliert werden.
$\bullet$: Memory und Rechnen sind kombiniert in jedem künstlichen Neuron
$\bullet$: das Netzwerk kann aus Erfahrung lernen (mittels einem ``Lernalgorithmus")
$\bullet$: es ist überwiegend ``demokratischßtrukturiert und hat eine parallele Arbeitsweise
$\bullet$: Rhythmus durch zentralen Taktgeber vorgegeben
$\bullet$: Kommunikation mittels Bits (oder Zahlen).

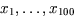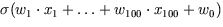**Abbildung 1:** Schematische Arbeitsweise eines künstlichen Neurons. Der Input besteht in diesem Fall aus 100 Input Zahlen $x_1,\ldots,x_{100}$ (wobei die Zahl 100 willkürlich gewählt wurde; ein biologisches Neuron erhält bis zu 10 000 Input Zahlen). Der Output besteht aus einer einzigen Zahl zwischen 0 und 1, die in der Zeichnung mit $\sigma(w_1 \cdot x_1 + \ldots + w_{100} \cdot x_{100} + w_0)$ bezeichnet ist. 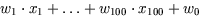Sie entsteht also dadurch, daß man zunächst die gewichtete Summe $w_1 \cdot x_1+ \ldots +w_{100}\cdot x_{100}+w_0$ berechnet, und auf diese Zahl dann die Quetschungsfunktion 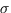$\sigma$ anwendet.
$\begin{figure}\vspace{1cm} \begin{center}\psfrag{X1}[B][B]{\footnotesize$x_1$... ... \cdot x_{100}+w_0)$}\epsfig {file=ray.eps, width=8cm}\end{center}\end{figure}$

Die Arbeitsweise eines künstlichen Neurons ist recht einfach. Wir betrachten als Beispiel ein künstliches Neuron mit 100 Input-Variablen 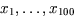$x_1,\ldots,x_{100}$ , die Bits oder reelle Zahlen repräsentieren können (siehe Abbildung 1).

Der Output 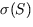$\sigma(S)$ eines künstlichen Neurons entsteht dadurch, daß es zunächst eine geeignete gewichtete Summe

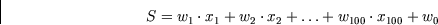
$\begin{displaymath}S = w_1 \cdot x_1 + w_2 \cdot x_2 + \ldots + w_{100} \cdot x_{100}+ w_0~\end{displaymath}$

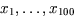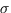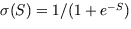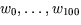der Inputs $x_1,\ldots,x_{100}$ ausrechnet, und dann eine sogenannte ``Quetschungsfunktion'' $\sigma$ auf diese gewichtete Summe S anwendet (zum Beispiel $\sigma(S) = 1/(1+e^{-S})$ ). Die Gewichte $w_0, \ldots, w_{100}$ sind Zahlen, die das gelernte Wissen des künstlichen Neurons repräsentieren. Zum Beispiel, w₁₇ ist eine große positive Zahl, wenn das Neuron die ``Erfahrung´´ gemacht hat, daß es einen relativ großen Output-Wert geben sollte, falls sein Input x₁₇ groß ist, und w₅₁ ist eine negative Zahl, wenn ein hoher Wert von x₅₁ zu einem niedrigen Output-Wert des Neurons führen soll ( siehe den folgenden Unterabschnitt 2.3.2). Der konstante Term w₀ legt gewissermaßen die ``Reizschwelle'' des künstlichen Neurons fest, also er legt fest wie hoch die Summe 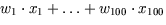$w_1 \cdot x_1 + \ldots + w_{100}\cdot x_{100}$ werden muß, damit der Output 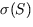$\sigma(S)$ einen hohen Wert ergibt.

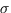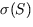Die nichtlineare Quetschungsfunktion $\sigma$ transformiert die oft stark positive oder stark negative Zahl S in eine Zahl $\sigma(S)$ zwischen 0 und 1 (Änderung des Maßstabs), siehe Abbildung 2.

**Abbildung 2:** Quetschungsfunktion 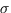$\sigma$ (die skizzierte Funktion ist die Funktion 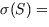$\sigma (S) =$ 1/(1+e^-S)).
$\begin{figure} \begin{center}\psfrag{S}[B][B]{$S$}\psfrag{sigS}[B][B]{$\sigma... ...phics [keepaspectratio,width=0.8\textwidth]{sig-new.eps}\end{center}\end{figure}$

Diese Änderung des Maßstabs ist nicht-linear, weil die Randbereiche mehr zusammengestaucht werden als der Mittelbereich.

Wie verbindet man die ``Neuronen'' in einem künstlichen Neuronalen Netz?

Ein einzelnes künstliches Neuron kann, selbst bei beliebiger Wahl der Gewichte 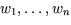$w_{1},\ldots, w_{n}$ und der Reizschwelle w₀, nur ein beschränktes Repertoire von Funktionen berechnen. Wenn man diesen Berechnungsvorgang aber iteriert, also den Output von einer Gruppe von Neuronen zum Input eines darauffolgenden weiteren Neurons macht (welches in der Regel andere Gewichte verwendet), so kann das so entstandene Netzwerk von künstlichen Neuronen (siehe Abbildungen 3 und 4) praktisch beliebig komplizierte Abbildungen von Inputs zu Outputs berechnen, oder vielmehr zu berechnen ``lernen'', wie wir im folgenden Unterabschnitt sehen.

**Abbildung:** Verbindungsstruktur eines typischen in einer Richtung ausgerichteten (``feedforward'') Neuronalen Netzes. Die Richtung der Berechnung in diesem Neuronalen Netz geht von links nach rechts. Jeder Punkt auf den Schichten 1,2,3, zusammen mit den in diesen Punkt gerichteten Pfeilen, symbolisiert ein künstliches Neuron wie in Abb. 1. Die Inputs der Neuronen auf Schicht 1 bestehen aus Netzwerk Inputs 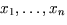$x_1,\ldots,x_n$ . Im 1. Zeitschritt berechnen alle Neuronen auf Schicht 1 gleichzeitig (``parallel'') ihre jeweilige Output Zahl. Die drei von den Neuronen auf Schicht 1 berechneten Output Zahlen werden weiter verarbeitet von Neuronen auf Schicht 2, d.h. sie liefern die Inputs für Neuronen auf Schicht 2. Die Neuronen auf Schicht 2 errechnen ihre Output Zahlen während dem 2. Zeitschritt, und aus diesen berechnet dann das Neuron auf Schicht 3 seinen Output, der gleichzeitig den Output des gesamten Neuronen Netzes (bestehend aus 7 Neuronen) bildet.
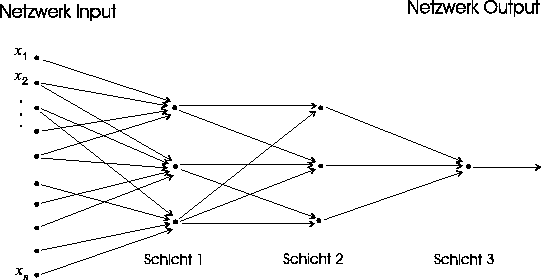$\begin{figure} \begin{center} \epsfig {file=108_3.eps,width=12cm} \end{center}\end{figure}$

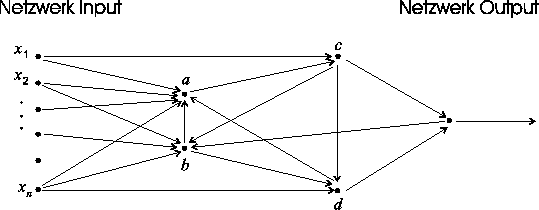
**Abbildung 4:** Beispiel für ein Neuronales Netz mit einer komplexeren Verbindungsstruktur. Der Netzwerk Input ist wieder links abgebildet, und der Netzwerk Output ist wieder rechts. Intern ist der Informationsfluß aber komplizierter. Das Neuron a erhält als Inputs nicht nur Netzwerk Inputs, sondern auch die Outputs der Neuronen b und d. Die Neuronen b und d bekommen als Input unter anderem den Output von Neuron c, das wiederum den Output von Neuron a als Input bekommt. Wegen der vielfältigen ``Rückkopplung'' im Netz ist es nicht mehr so einfach zu beschreiben, wie die einzelnen Rechenschritte im Netz koordiniert werden. Komplizierte Netzwerk-Strukturen mit ``Rückkopplungen'' sind typisch für biologische Netzwerke von Neuronen, werden aber für eine große Anzahl von Anwendungen auch künstlich im Rechner simuliert.
$\begin{figure} \begin{center} \epsfig {file=108_4.eps,width=12cm} \end{center}\end{figure}$

Woher kommen die ``Gewichte'' in einem künstlichen Neuronalen Netz?

Die Gewichte und Reizschwellen w_i der künstlichen Neuronen in einem Neuronalen Netz sind Zahlen, die das ``Programmëines Neuronalen Netzes enthalten, also seine Arbeitsweise festlegen. Anstatt die Werte der Gewichte und Reizschwellen fest einzuprogrammieren, überläßt man es dem Neuronalen Netz, deren Werte selbst so zu wählen, daß es das gewünschte Input/Output-Verhalten zeigt. Dazu wird es mit Trainingsbeispielen für ``gute'' Kombinationen von Inputs und Outputs gefüttert. Mittels einem einprogrammierten Lernalgorithmus kann es diese Trainingsbeispiele benutzen um seine Gewichte und Reizschwellen, und damit seine Arbeitsweise, in geeigneter Weise zu verändern.

Man verwendet unter anderem die folgenden Design Ideen bei der Konstruktion von Lernalgorithmen für künstliche neuronale Netze:

$\bullet$: Ermittle für jedes Gewicht in welcher Richtung man es verändern soll, damit das Verhalten des Neuronalen Netzes ``in die richtige Richtung" verändert wird
$\bullet$: Geduld: Viele richtige kleine Schritte bei Änderungen von Gewichten und Reizschwellen führen auch zum Ziel
$\bullet$: Sei gelegentlich ``kreativ", z.B. probier einfach aus, was passiert, wenn man einem Gewicht einen ganz anderen Wert gibt ( 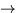$\rightarrow$ Zufallselemente).

Was leistet ein künstliches Neuronales Netz?

Mit genügend vielen Trainingsbeispielen kann ein Neuronales Netz zum Beispiel lernen

$\bullet$: handgeschriebene Zeichen zu lesen
$\bullet$: dem Arzt bei der Diagnose von Krankheiten zu helfen (z.B. Früherkennung von Brustkrebs)
$\bullet$: einen Motor so zu steuern, daß der Ausstoß von Schadstoffen minimiert wird
$\bullet$: einen Roboter so zu steuern, daß er Kollisionen mit Hindernissen vermeidet.

Abgesehen von ihrer Lernfähigkeit haben Neuronale Netze den Vorteil, daß alle praktisch wichtigen Funktionen mittels in einer Richtung ausgerichteten Netzen bestehend aus nur 2 Schichten (und daher in nur 2 parallelen Rechenschritten) mit nicht zu vielen künstlichen Neuronen berechnet werden können. Daher ergeben Neuronale Netze gleichzeitig ein sehr nützliches mathematisches Modell für Rechnen in ``Echtzeit''.^[Links]

Wie unterscheidet sich ein künstliches Neuronales Netz von seinem Vorbild in der Natur?

Wenn man die Arbeitsweise und Leistung der gegenwärtigen Generation von künstlichen Neuronalen Netzen mit der von biologischen Nervensystemen vergleicht, stellt sich heraus, daß sie weiter voneinander entfernt sind, als man früher gedacht hatte. Ein wesentlicher Unterschied zwischen biologischen und künstlichen Neuronen liegt in der Struktur ihres Outputs. Der Output eines biologischen Neurons besteht aus elektrischen Pulsen (``spikes''), die in unregelmäßigen Abständen, ca 1-100 mal pro Sekunde, ausgesendet werden. Wenn man

**Abbildung:** Aufnahme der Feuerzeiten von 30 Neuronen in der visuellen Kortex des Affen über 4 Sekunden [Krüger and Aiple, 1988]. Die 30 Neuronen wurden von den Experimentatoren mit A1 bis E6 bezeichnet (siehe linke Spalte der Abbildung). Das Feuerverhalten von jedem der 30 Neuronen ist jeweils in einer Zeile protokolliert. Die waagrechte Achse ist die Zeitachse. Jede Feuerzeit ist durch einen senkrechten Strich angezeigt. Man bezeichnet die jeweils in einer Zeile festgehaltene Folge von Feuerzeichen eines Neurons als ``spike train''. Zum Vergleich mit der Zeitdauer einer typischen Berechnung in einem Nervensystem haben wir ein Zeitintervall von 150 Millisekunden grau markiert. Innerhalb dieser Zeitdauer können biologische Nervensysteme (bestehend aus 10 und mehr Schichten) komplexe Aufgaben der Musterkennung ausführen. Abdruck mit freundlicher Genehmigung von The Amercian Physiological Society.
$\begin{figure}\begin{center} \includegraphics [keepaspectratio,width=11.6cm]{97_2.eps}\end{center}\end{figure}$

die Zeiten protokolliert, wann ein biologisches Neuron einen spike aussendet, so schaut ein solcher ``spike train'' so aus wie eine der Zeilen von Abbildung 5. In Abbildung 5 wurden die spike trains von 30 (ziemlich willkürlich ausgewählten) Neuronen für einen Zeitraum von 4 Sekunden aufgezeichnet. Wenn wir zum Beispiel alle Informationen protokollieren würden, die unser Gehirn innerhalb von 4 Sekunden von unseren Augen erhält, so würde eine ähnliche Abbildung mit 1.000.000 Zeilen (anstatt 30) entstehen, weil alle visuellen Eindrücke in der Retina in die spike trains von 1.000.000 Neuronen kodiert und in dieser Form über den optischen Nerven an das Gehirn weitergeleitet werden.

Man hat früher gemeint, daß das einzige relevante Signal im Output eines biologischen Neurons die Häufigkeit seines Feuerns ist, und daß diese Häufigkeit dem Output 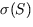$\sigma(S)$ eines künstlichen Neurons entspricht. Man sieht aber sofort aus Abbildung 5, daß sich die momentane Häufigkeit des Feuerns eines biologischen Neurons ständig ändert, und daß die zeitlichen Abstände zwischen dem Feuern eines Neurons viel zu unregelmäßig sind um aus 2 oder 3 spikes eine gute Abschätzung von dessen gegenwärtiger Häufigkeit des Feuerns zu ermöglichen. Neuere experimentelle Untersuchungen (siehe zum Beispiel [Rieke et al., 1997,Koch, 1999,Recce, 1999]) zeigen vielmehr, daß das gesamte raum-zeitliche Muster des Feuerns von biologischen Neuronen für deren Informationsverarbeitung relevant ist. Man kann den Output eines Systems von biologischen Neuronen also eher mit einem von einem großen Orchester gespielten Musikstück vergleichen, zu dessen Wiedererkennung es nicht ausreicht zu wissen wie oft jedes Instrument gewisse Töne spielt. Charakteristisch für ein Musikstück ist vielmehr, wie jeder Ton in eine Melodie oder in einen Akkord eingebettet ist. Man nimmt an, daß in ähnlicher Weise viele Gruppen von Neuronen in biologischen Systemen die von ihnen ausgesendeten Informationen durch das zeitliche Muster kodieren, in dem jedes Neuron in der Gruppe relativ zu den anderen feuert. Daher ist die Kommunikationsweise innerhalb unseres Gehirns einem Musikstück sehr viel ähnlicher als die von der gegenwärtigen Generation von Computern bevorzugte Kommunikationsweise.

Die Untersuchung der theoretischen und praktischen Möglichkeiten mittels raum-zeitlicher Muster von Pulsen zu rechnen und zu kommunizieren, hat in den letzten Jahren eine neue Generation künstlicher Neuronaler Netzwerke enstehen lassen: pulsbasierte künstliche Neuronale Netze.^[Kommentar] In diesen wird die künstliche Synchronisation der traditionellen künstlichen Neuronalen Netzen ersetzt durch die der Biologie abgeschaute Methode, Informationen in raum-zeitlichen Mustern (analog wie bei einem Handzeichen oder einer Melodie) zu kodieren. Dies eröffnet für den Informatiker eine faszinierende neue Welt, nämlich die Möglichkeit Zeit als eine bisher in unseren Rechnern brachliegende Dimension zu erschließen, und direkt mit raum-zeitlichen Mustern zu rechnen [Maass, 1999,Maass and Sontag, 1999].^[Link]

Erfreulicherweise kann man diese Strategie auch relativ leicht in neu entwickelter elektronischer Hardware anwenden [Murray, 1999].^[Kommentar] Diese Kodierungsstrategie implementiert eine faszinierende Idee von [Mead, 1989]: ``to let time represent itself'', d.h. anstatt die zeitliche Struktur der Inputs (zum Beispiel visuelle Informationen über bewegte Objekte) durch angehängte künstliche ``time-stamps'' - vergleichbar den Eingangsstempeln in einem Büro - zu kodieren, bleibt die zeitliche Struktur des Inputs während des ``Rechnens'' in der raum-zeitlichen Struktur der spike trains repräsentiert. In einer Analogie kann man diese Vorgangsweise vergleichen mit der Arbeitsweise in der Küche eines (noch nicht vollständig digitalisierten) Restaurants. Dort werden die vom Ober aufgenommenen Bestellzettel für die Köche gut sichtbar an einem Rad (oder gelegentlich an einer Schiene) befestigt. In diesem Fall kodiert die Position jedes einzelnen Bestellzettels relativ zu den anderen die Zeit seines Eingangs. Auch ohne Eingangsstempel (``time stamps'') auf den Bestellzetteln können bei dieser raum-zeitlichen Organisationsstruktur die Bestellungen in der richtigen Reihenfolge ausgeführt werden. Der Ansatz, daß man traditionelle Rechenschritte ersetzt durch geeignete Manipulationen von raum-zeitlichen Strukturen, eröffnet neue Möglichkeiten um zum einen Energie-effiziente parallele Rechner zur Verarbeitung komplexer Information in Echtzeit zu entwerfen, und zum anderen möglicherweise ein wenig besser zu verstehen wie komplexe raum-zeitliche Informationen im menschlichen Gehirn kodiert und verarbeitet werden.^[Links]

[Next][Up][Previous]
Next:KonklusionUp:Das Menschliche Gehirn -Previous:Einführung

Heike Graf, 9/28/1999