|

|
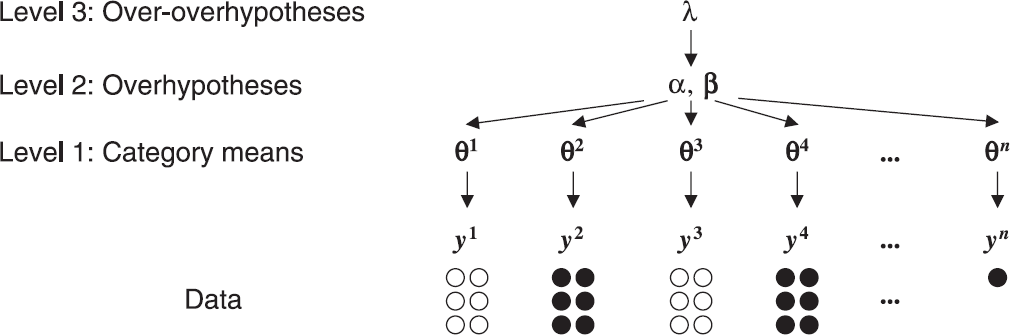
Apply Gibbs sampling to acquire overhypotheses about the feature
variability for the bags of marbles model illustrated in Fig. 9:
Suppose that ![]() is a stack containing many bags of marbles. We empty several bags and discover that the marbles within the same bag have certain features in common: For instance some bags may contain black marbles, others may contain white marbles, but that the marbles in each bag are uniform in color. Given a new bag - bag
is a stack containing many bags of marbles. We empty several bags and discover that the marbles within the same bag have certain features in common: For instance some bags may contain black marbles, others may contain white marbles, but that the marbles in each bag are uniform in color. Given a new bag - bag ![]() - and a single marble (e.g. a black marble) drawn from this bag we are interested in the probability of the colors of all other marbles within this bag. On its own, a single draw would provide little information about the contents of the new bag, but experience with previous bags may lead us to endorse certain hypothesis (e.g. all marbles in a bag have uniform colors).
- and a single marble (e.g. a black marble) drawn from this bag we are interested in the probability of the colors of all other marbles within this bag. On its own, a single draw would provide little information about the contents of the new bag, but experience with previous bags may lead us to endorse certain hypothesis (e.g. all marbles in a bag have uniform colors).
Learning overhypothesis:
The term overhypothesis is used to refer to any form of abstract knowledge that sets up a hypothesis space at a less abstract level. By this criterion, an overhypothesis sets up a space of hypotheses about the marbles in bag ![]() : they could be uniformly black, uniformly
white, and so on. Hierarchical Bayesian models capture the notion of overhypothesis by allowing hypothesis spaces at several levels of abstraction. In this example we wish to explain how a certain kind of inference can be drawn from a given body of data. In this case, the data are observations of several bags and we are working with a set of
2 colors.
: they could be uniformly black, uniformly
white, and so on. Hierarchical Bayesian models capture the notion of overhypothesis by allowing hypothesis spaces at several levels of abstraction. In this example we wish to explain how a certain kind of inference can be drawn from a given body of data. In this case, the data are observations of several bags and we are working with a set of
2 colors.
Bags of marbles model:
Let ![]() indicate a set of observations of the marbles in bag
indicate a set of observations of the marbles in bag
![]() . If we have drawn five marbles from bag 7 and all but one are black, then
. If we have drawn five marbles from bag 7 and all but one are black, then
![]() . We are interested in the ability to predict the color of the next marble to be drawn from bag
. We are interested in the ability to predict the color of the next marble to be drawn from bag ![]() . The first step is to identify a kind of knowledge (level 1 knowledge) that explains the data and that supports the ability of interest. In this case, level 1 knowledge is knowledge about the color distribution of each bag. Let
. The first step is to identify a kind of knowledge (level 1 knowledge) that explains the data and that supports the ability of interest. In this case, level 1 knowledge is knowledge about the color distribution of each bag. Let
![]() indicate the true color distribution for
the
indicate the true color distribution for
the ![]() th bag in the stack.
We assume that
th bag in the stack.
We assume that ![]() is drawn from a binomial distribution
with parameter
is drawn from a binomial distribution
with parameter
![]() : in other words, the marbles
responsible for the observations in
: in other words, the marbles
responsible for the observations in ![]() are drawn independently
at random from the
are drawn independently
at random from the ![]() th bag, and the color of
each depends on the color distribution
th bag, and the color of
each depends on the color distribution
![]() for that bag.
If 60% of the marbles in bag 7
are black, then
for that bag.
If 60% of the marbles in bag 7
are black, then
![]() .
.
For the marbles scenario, level 2 knowledge is knowledge about
the distribution of the
![]() variables. This knowledge is represented using two parameters,
variables. This knowledge is represented using two parameters, ![]() and
and ![]() .
The vectors
.
The vectors
![]() are drawn from a Beta distribution
parameterized by a scalar
are drawn from a Beta distribution
parameterized by a scalar ![]() and a scalar
and a scalar ![]() . The parameter
. The parameter ![]() determines the extent to which the colors in each bag tend to be uniform, and
determines the extent to which the colors in each bag tend to be uniform, and ![]() represents the distribution of colors across the entire collection of bags.
We need to formalize our a priori expectations about the values of
these variables.
represents the distribution of colors across the entire collection of bags.
We need to formalize our a priori expectations about the values of
these variables.
Level 2 knowledge is acquired by relying on a body of knowledge at an even higher level, level 3.
We use a uniform distribution on ![]() and an exponential distribution on
and an exponential distribution on ![]() , which captures a weak
prior expectation that the marbles in any bag will tend
to be uniform in color. The mean of the exponential distribution is
, which captures a weak
prior expectation that the marbles in any bag will tend
to be uniform in color. The mean of the exponential distribution is
![]() , i.e.
, i.e.
![]() .
The parameter
.
The parameter ![]() and the pair
and the pair
![]() are both overhypotheses, since each
sets up a hypothesis space at the next level down. Since the level 3 knowledge is specified in advance (
are both overhypotheses, since each
sets up a hypothesis space at the next level down. Since the level 3 knowledge is specified in advance (![]() ), you should analyze how an overhypothesis can be learned at level 2.
), you should analyze how an overhypothesis can be learned at level 2.
The joint probability distribution for this model is therefore given by
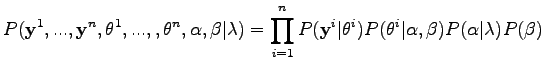 |
(1) |
| (2) | |||
| (3) | |||
| (4) | |||
| (5) |