If you pour water over your PC, the PC will stop working. This is because very late in the history of computing – which started about 500 million years ago¹ – the PC and other devices for information processing were developed that require a dry environment. But these new devices, consisting of hardware and software, have a disadvantage: they do not work as well as the older and more common computational devices that are called nervous systems, or brains, and which consist of wetware. These superior computational devices were made to function in a somewhat salty aqueous solution, apparently because many of the first creatures with a nervous system were coming from the sea. We still carry an echo of this history of computing in our heads: the neurons in our brain are embedded into an artificial sea-environment, the salty aqueous extracellular fluid which surrounds the neurons in our brain. The close relationship between the wetware in our brain, and the wetware in evolutionary much older organisms that still live in the sea, is actually quite helpful for research. Neurons in the squid are 100 to 1000 times larger than the neurons in our brain, and therefore easier to study. Nevertheless the equations that Hodgkin and Huxley derived to model the dynamics of the neuron that controls the escape reflex of the squid (for which they received the Nobel prize in 1963), also apply to the neurons in our brain. In this short paper I want to give you a glimpse at this foreign world of computing in wetware.

One of the technical problems that nature had to solve for enabling computation in wetware was how to communicate intermediate results from the computation of one neuron to other neurons, or to output-devices such as muscles. In a PC one sends streams of bits over copper wires. But copper wires were not available a few hundred million years ago, and they also do not work so well in a sea-environment. The solution that nature found was the so-called action potential or spike. The spike plays in a brain a similar role as a bit in a digital computer: it is the common unit of information in wetware.

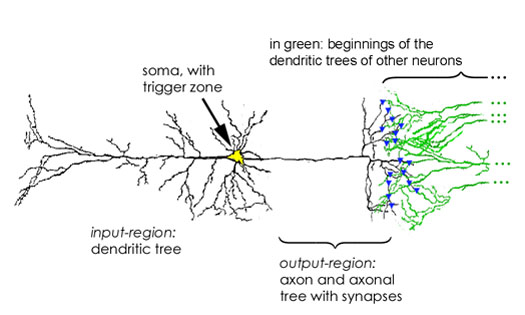
Figure 1: Simplified drawing of a neuron, with input region, the cell body or soma (the trigger zone lies at its right end of the soma, just where the axon begins), and output region. Synapses are indicated by blue triangles.

A spike is a sudden voltage increase for about 1 ms (1 ms = 1/1000 second) that is created at the cell body (soma) of a neuron, more precisely at its trigger zone, and propagated along a lengthy fiber (called axon) that extends from the cell body. This axon corresponds to an insulated copper wire in hardware. The gray matter of your brain contains a large amount of such axons: about 4 km in every cubic millimeter ( = 1 mm³). Axons have numerous branching points (see the axonal tree on the right hand side of Fig. 1), at which most spikes are automatically duplicated, so that they can enter each
 
 

 

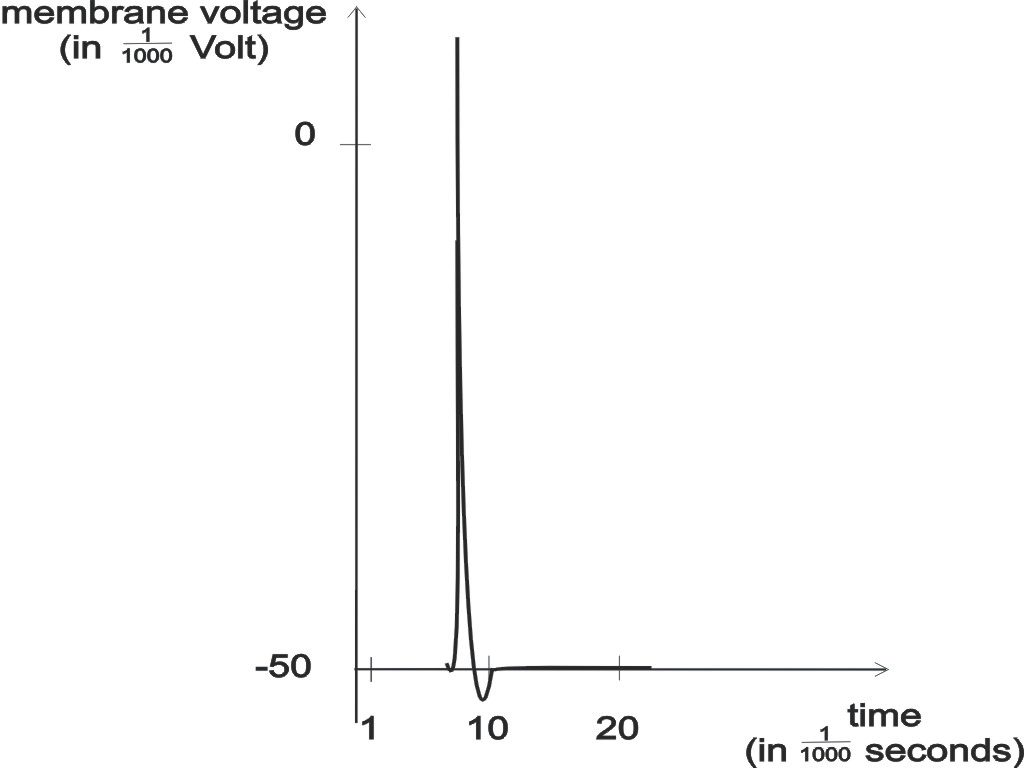
Figure 2: Time cause of an action potential at the soma of a neuron.

branch of the axonal tree. In this way a spike from a single neuron can be transmitted to a few thousand other neurons. But in order to move from one neuron to another, the spike has to pass a rather complicated switch, a so-called synapse (marked by a blue triangle in Figure 2, and shown in more detail in Figure 3).
 
 

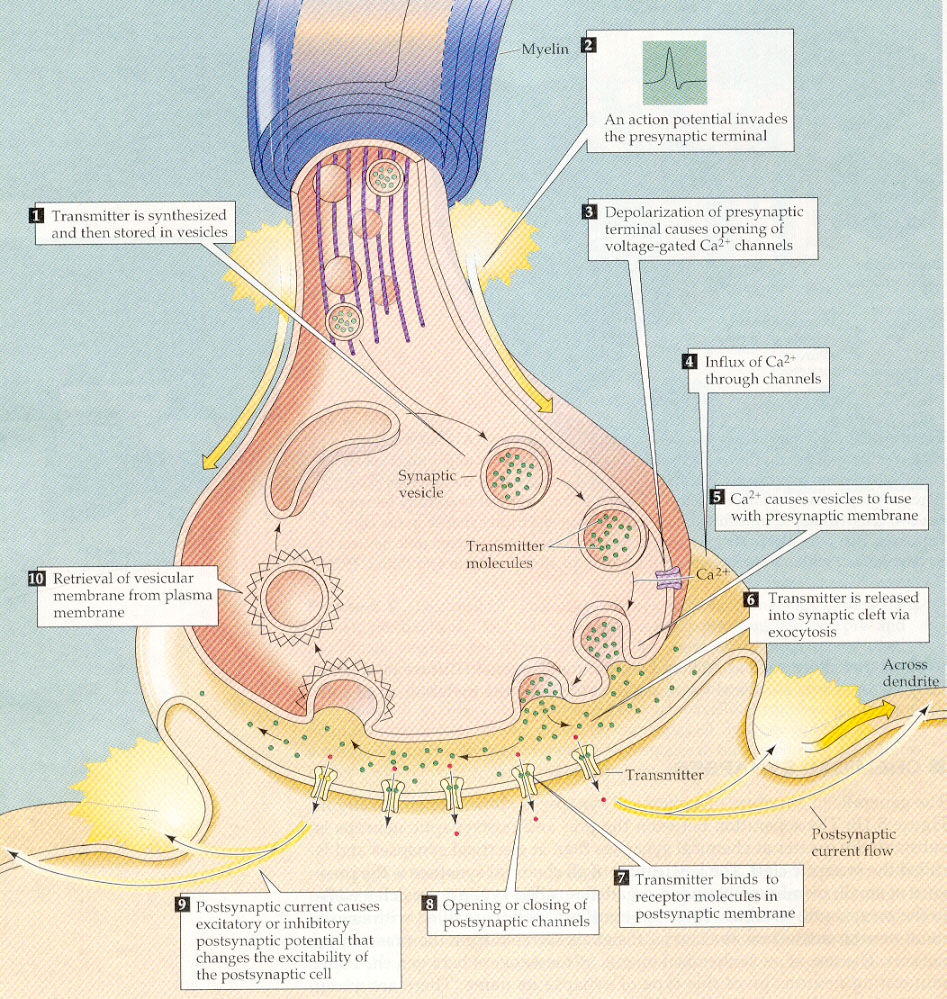
Figure 3: The spike enters the presynaptic terminal, which is an endpoint of the axonal tree of the preceding neuron, shown on the top. It may cause a vesicle filled with neurotransmitter to fuse with the cell membrane, and to release its neurotransmitter molecules into the small gap (synaptic cleft) to the cell membrane of the next neuron (called postsynaptic neuron in this context), which is shown at the bottom. If the neurotransmitter reaches a receptor of the postsynaptic neuron, a channel will be opened that lets charged particles pass into the postsynaptic neuron. Empty vesicles are recycled by the presynaptic terminal.

When a spike enters a synapse, it is likely to trigger a complex chain of events that are indicated in Figure 3 ²: a small vesicle filled with special molecules ("neurotransmitter") is fused with the cell membrane of the presynaptic terminal, thereby releasing the neurotransmitter into the extracellular fluid. Whenever a neurotransmitter molecule reaches a particular molecular arrangement (a "receptor") in the cell membrane of the next neuron, it will open a channel in that cell membrane through which charged particles (ions) can enter the next cell. This causes an increase or decrease (depending on the type of channel that is opened and the types of ions that this channel lets through) of the membrane voltage by a few millivolt (1 millivolt = 1/1000 volt).
 
 

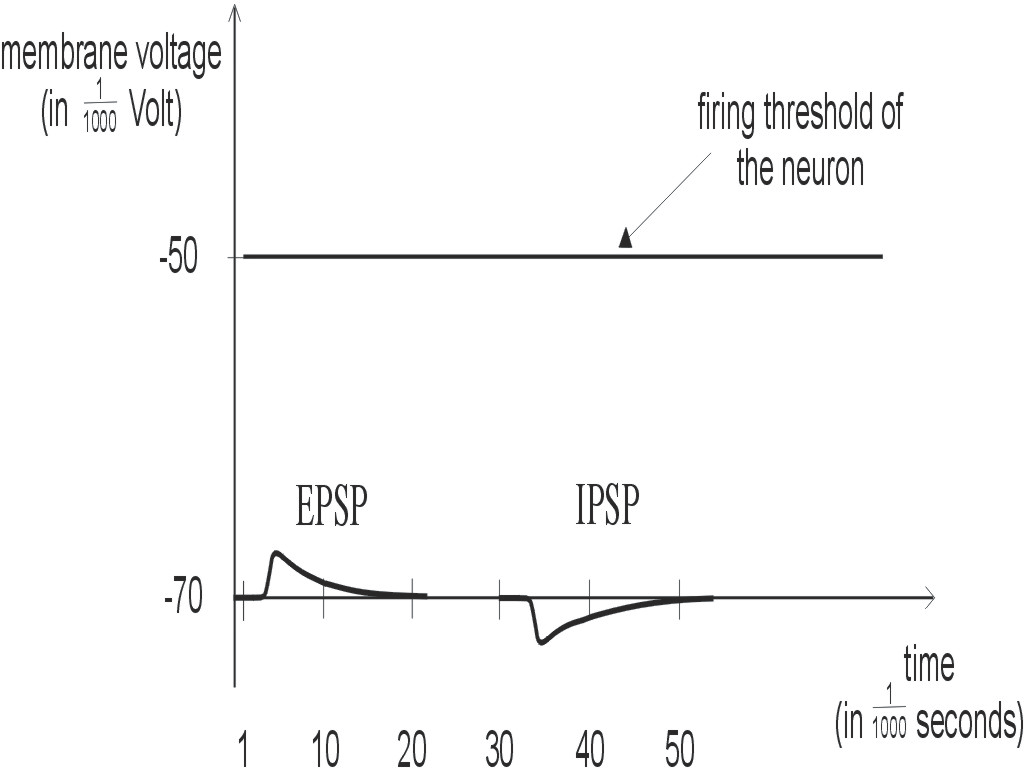
Figure 4: Postsynaptic potentials are either excitatory (EPSP) or inhibitory (IPSP). The membrane voltage is a sum of many such postsynaptic potentials. As soon as this sum reaches the firing threshold, the neuron fires.

One calls these potential changes EPSPs (excitatory postsynaptic potentials) if they increase the membrane voltage, and otherwise IPSPs (inhibitory postsynaptic potentials). In contrast to the spikes, which all look alike, the size and shape of these postsynaptic potentials depends very much on the particular synapse that causes it. In fact it will also depend on the current "mood" and the recent "experiences" of this synapse, since the postsynaptic potentials have different sizes, depending on the pattern of spikes that have reached the synapse in the past, on the interaction of these spikes with the firing activity of the postsynaptic neuron, and also on other signals that reach the synapse in the form of various molecules (e.g. neurohormones) through the extracellular fluid.

Sometimes people wonder whether it is possible to replace wetware by hardware, to replace for example parts of a brain by silicon chips. This is not so easy because wetware does not consist of fixed computational components, like a silicon chip, that perform the same operation in the same way on every day of their working life. Instead the channels and receptors of neurons and synapses move around, disappear, and are replaced by new and possibly different receptors and channels that are continuously reproduced by a living cell in dependence of the individual "experience" of that cell (such as the firing patterns of the pre- and postsynaptic neuron, and the cocktail of biochemical substances that reach the cell through the extracellular fluid). This implies that next year a synapse in your brain is likely to perform its operations quite differently from today, whereas a silicon clone of your brain would be stuck with the "old" synapses from this year.

The postsynaptic potentials created by the roughly 10.000 synapses converging on a single neuron are transmitted by a tree of input wires ("dendritic tree", see Fig. 2) to the trigger zone at the cell body of a neuron. Whenever the sum of these hundreds and thousands of continuously arriving voltage changes reaches there the firing threshold, the neuron will "fire" (a chain reaction orchestrated through the rapid opening of channels in the cell membrane that allow positively charged sodium ions to enter the neuron, thereby increasing the membrane voltage, which causes further channels to open) and send out a spike through its axon.³ So we are back at our starting point, the spike.

The question is now how a network of neurons can compute with such spikes. Figure 5 presents an illustration of a tiny network consisting of just 3 neurons, which communicate via sequences of spikes (usually referred to as spike trains).
 
 

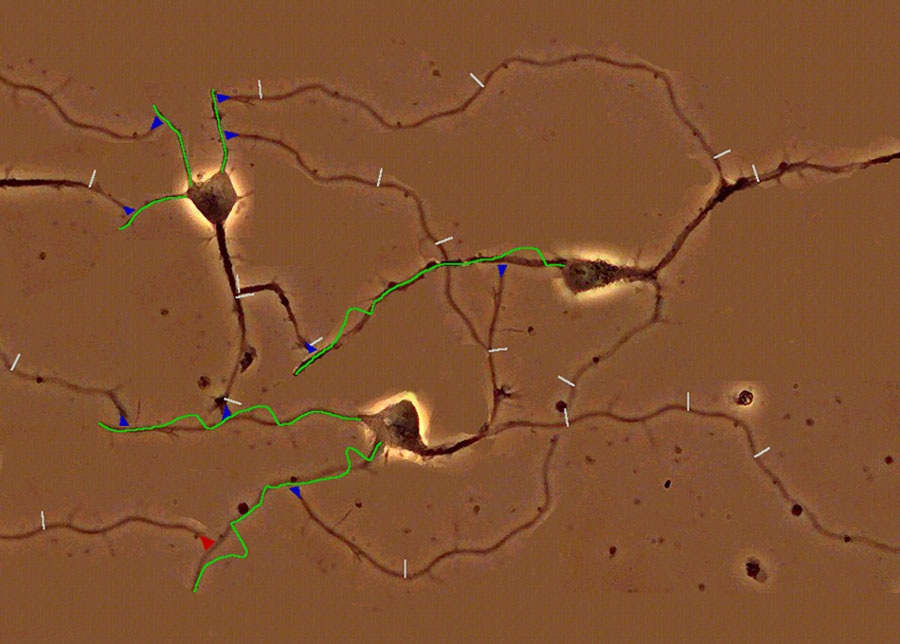
Figure 5: A simulated network of 3 neurons. Postsynaptic potentials in the input regions of the neurons (dendritic tree) are indicated by green curves. Spikes are indicated by white bars on the axons, and synapses by blue triangles. In the online available computer installation you can create your own input spike train, and watch the response of the network. You can also change the strength of the synapses, a process that may correspond to learning in your brain.
See [Maass, 2000], (https://igi-web.tugraz.at/people/maass/118/118.html) for more detailed information.

It is taken from an animated computer installation which is online available. It allows you to create your own spike train, and watch how the network responds to it. You can also change the strength of the synapses, and thereby simulate (in an extremely simplified manner) processes that take place when the neural system "learns".⁴ But we still do not know how to transmit information via spikes, hence let us look at the protocol of a real computation in wetware.

In Figure 6 the spike trains emitted by 30 (randomly selected) neurons in the visual area of a monkey brain are shown for a period of 4 seconds. All information of your senses, all your ideas and thoughts are coded in a similar fashion by spike trains. If you would for example make a protocol of all
 
 

Figure 6: Recording of spike trains from 30 neurons in the visual cortex of a monkey over 4 seconds. The 30 neurons were labeled A1 – E6 (the labels are given on the left of the figure). The spike train emitted by each of the neurons is recorded in a separate row. Each point in time when a neuron fires and thereby emits a spike is marked by a small vertical bar. Hence one read this figure like a music score. The time needed for a typical fast computation in our brain is marked in gray; these are 150ms. Within this time our brain can solve quite complex information processing problems, like for example the recognition of a face. Currently our computers would need a substantially longer computation time for such tasks.

the visual information which reaches your brain within 4 seconds, you would arrive at a similar figure, but with 1.000.000 rows instead of 30, because the visual information is transmitted from the retina of your eye to your brain by the axons of about 1.000.000 neurons.

Researchers used to think that the only computationally relevant signal in the output of a neuron was the frequency of its firing. But you may notice in Figure 6 that the frequency of firing of a neuron tends to change rapidly, and that the temporal distances between the spikes are so irregular that you have a hard time estimating the average frequency of firing of a neuron by looking at just 2 or 3 spikes from that neuron. On the other hand our brain can compute quite fast, in about 150 ms, with just 2 or 3 spikes per neuron. Hence other features of spike trains must be used by the brain for transmitting information. Recent experimental studies (see for example [Rieke et al., 1997, Koch 1999, Recce 1999]) show that in fact the full spatial and temporal pattern of spikes emitted by neurons is relevant for the message which they are sending to other neurons. Hence it would be more appropriate to compare the output of a collection of neurons with a piece of music played by an orchestra. To recognize such piece of music it does not suffice to know how often each note is played by each musician. Instead we have to know how the notes of the musicians are embedded into the melody and into the pattern of notes played by other musicians. One assumes now that in a similar manner many groups of neurons in the brain code their information through the pattern in which each neuron fires relative to the other neurons in the group. Hence, one may argue that music is a code that is much closer related to the codes used in your brain than the bit-stream code used by a PC.

The investigation of theoretical and practical possibilities to compute with such spatio-temporal patterns of pulses has lead to the creation of a new generation of artificial neural networks, so-called pulsbased neural networks (see [Maass, Bishop] for surveys and recent research results). Such networks are appearing now also in the form of novel electronic hardware [Mead, 1989, Deiss et al, 1999, Murray, 1999]. An interesting feature of these pulsbased neural networks is that they do not require a global synchronisation (like a PC , or a traditional artificial neural network). Hence they allow to use time as a new dimension for coding information. In addition they can save a lot of energy⁵, since no clock signal has to be transmitted all the time to all components of the network .One big open problem is the organization of computation in such systems, since the operating system of wetware is still unknown, even for the squid. Hence our current research, jointly with neurobiologists, concentrates on unraveling the organization of computation in neural microcircuits, the lowest level of circuit architecture in the brain (see [Maass, Natschlaeger, and Markram]).
 

Footnotes:

¹ One could also argue that the history of computing started somewhat earlier, even before there existed any nervous systems: 3 to 4 billion years ago when nature discovered information processing via RNA.

² See http://www.wwnorton.com/gleitman/ch2/tutorials/2tut5.htm for an online animation.

³ See http://www.wwnorton.com/gleitman/ch2/tutorials/2tut2.htm for an online animation.

⁴ See http://www.igi.TUGraz.at/demos/index.html. This computer installation was programmed by Thomas Natschlaeger and Harald Burgsteiner, with support from the Steiermaerkische Landesregierung. Detailed explanations and instructions are online available from https://igi-web.tugraz.at/people/maass/118/118.html, see [Maass, 2000b]. Further background information is online available from [Natschlaeger, 1996], [Maass, 2000a], [Maass, 2001].

⁵ Wetware consumes much less energy than any hardware that is currently available. Our brain, which has about as many computational units as a very large supercomputer, consumes just 10 to 20 Watt.
 
 
 

References

Deiss, S. R., Douglas, R. J., and Whatley, A. M. (1999). A pulse-coded communications infrastructure for neuromorphic systems. In Maass, W., and Bishop, C., editors, Pulsed Neural Networks. MIT-Press, Cambridge.

Koch, C. (1999). Biophysics of Computation: Information Processing in Single Neurons. Oxford University Press (Oxford).

Krüger, J., and Aiple, F. (1988). Multielectrode investigation of monkey striate cortex: spike train correlations in the infragranular layers. Neurophysiology, 60:798-828.

Maass, W. (2000a). Das menschliche Gehirn – nur ein Rechner?. In Burkard, R. E., Maass, W., and P. Weibel, editors, Zur Kunst des Formalen Denkens, pages 209-233. Passagen Verlag (Wien), 2000.
See #108 on https://igi-web.tugraz.at/people/maass/publications.html

Maass, W. (2000b). Spike trains – im Rhythmus neuronaler Zellen. In Kriesche, R., and Konrad, H., editors, Katalog der steirischen Landesausstellung gr2000az, pages 36-42. Springer Verlag.
See #118 on https://igi-web.tugraz.at/people/maass/publications.html

Maass, W. (2001). Paradigms for computing with spiking neurons. In Leo van Hemmen, editor, Models of Neural Networks, volume 4. Springer (Berlin), to appear.
See #110 (Gzipped PostScript) on https://igi-web.tugraz.at/people/maass/publications.html

Maass, W., and Bishop, C., editors (1999). Pulsed Neural Networks. MIT-Press (Cambridge, MA). Paperback (2001).
See https://igi-web.tugraz.at/people/maass/PNN.html

Maass, W., Natschlaeger, T., and Markram, H. (2001). Real-time computing without stable states: a new framework for neural computation based on perturbations, submitted for publication.

Mead, C. (1989). Analog VLSI and Neural Systems. Addison-Wesley (Reading).

Murray, A. F. (1999). Pulse-based computation in VLSI neural networks. In Maass, W., and Bishop, C., editors, Pulsed Neural Networks. MIT-Press (Cambridge, MA).

Natschläger, T. (1996). Die dritte Generation von Modellen für neuronale Netzwerke Netzwerke von Spiking Neuronen. In: Jenseits von Kunst. Passagen Verlag. See http://www.igi.tugraz.at/tnatschl/

Recce, M. (1999). Encoding information in neuronal activity. In Maass, W., and Bishop, C., editors, Pulsed Neural Networks. MIT-Press (Cambridge, MA).

Rieke, F., Warland, D., Bialek, W., and de Ruyter van Steveninck, R. (1997). SPIKES: Exploring the Neural Code. MIT-Press (Cambridge, MA).