Circuits composed of threshold gates (McCulloch-Pitts neurons, or perceptrons)
are simplified models of neural circuits with the advantage that they are
theoretically more tractable than their biological counterparts. However,
when such threshold circuits are designed to perform a specific computational
task they usually differ in one important respect from computations in the
brain: they require very high activity. On average every second threshold
gate fires (sets a ``1'' as output) during a computation. By contrast, the
activity of neurons in the brain is much more sparse, with only about 1% of
neurons firing. This mismatch between threshold and neuronal circuits is due
to the particular complexity measures (circuit size and circuit depth) that
have been minimized in previous threshold circuit constructions. In this
article we investigate a new complexity measure for threshold circuits,
energy complexity, whose minimization yields computations with sparse
activity. We prove that all computations by threshold circuits of polynomial
size with entropy
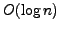
can be restructured so that their energy
complexity is reduced to a level near the
entropy of circuit states.
This entropy of circuit states is a novel circuit complexity measure, which
is of interest not only in the context of threshold circuits, but for circuit
complexity in general. As an example of how this measure can be applied we
show that any polynomial size threshold circuit with entropy
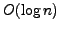
can
be simulated by a polynomial size threshold circuit of depth 3. Our results
demonstrate that the structure of circuits which result from a minimization
of their energy complexity is quite different from the structure which
results from a minimization of previously considered complexity measures, and
potentially closer to the structure of neural circuits in the nervous system.
In particular, different pathways are activated in these circuits for
different classes of inputs. This article shows that such circuits with
sparse activity have a surprisingly large computational power.