C. Papadimitriou, S. Vempala, D. Mitropolsky, M. Collins, and W. Maass
Assemblies are large populations of neurons believed to imprint memories,
concepts, words and other cognitive information. We identify a repertoire of
operations on assemblies. These operations correspond to properties of
assemblies observed in experiments, and can be shown, analytically and
through simulations, to be realizable by generic, randomly connected
populations of neurons with Hebbian plasticity and inhibition. Operations
on assemblies include: projection (duplicating an assembly by creating a new
assembly in a downstream brain area); reciprocal projection (a variant of
projection also entailing synaptic connectivity from the newly created
assembly to the original one); association (increasing the overlap of two
assemblies in the same brain area to reflect cooccurrence or similarity of
the corresponding concepts); merge (creating a new assembly with ample
synaptic connectivity to and from two existing ones); and pattern-completion
(firing of an assembly, with some probability, in response to the firing of
some but not all of its neurons). Our analytical results establishing the
plausibility of these operations are proved in a simplified mathematical
model of cortex: a finite set of brain areas each containing
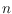
excitatory
neurons, with random connectivity that is both recurrent (within an area) and
afferent (between areas). Within one area and at any time, only
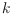
of the
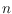
neurons fire an assumption that models inhibition and serves to define
both assemblies and areas while synaptic weights are modified by Hebbian
plasticity, as well as homeostasis. Importantly, all neural apparatus needed
for the functionality of the assembly operations is created on the flythrough
the randomness of the synaptic network, the selection of the
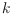
neurons with
the highest synaptic input, and Hebbian plasticity, without any special
neural circuits assumed to be inplace. Assemblies and their operations
constitute a computational model of the brain which we call the Assembly
Calculus, occupying a level of detail intermediate between the level of
spiking neurons and synapses, and that of the whole brain. As with high-level
programming languages, a computation in the Assembly Calculus (that is, a
coherent sequence of assembly operations accomplishing a task) can ultimately
be reduced “compiled down” to computation by neurons and synapses; however,
it would be far more cumbersome and opaque to represent the same computation
that way. The resulting computational system can be shown, under assumptions,
to be in principle capable of carrying out arbitrary computations. We
hypothesize that something like it may underlie higher human cognitive
functions such as reasoning, planning,and language. In particular, we propose
a plausible brain architecture based on assemblies for implementing the
syntactic processing of language in cortex, which is consistent with recent
experimental results.