Neural nets with superlinear VC-dimension

W. Maass

Abstract:

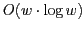
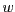
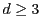
It has been known for quite a while that the Vapnik-Chervonenkis dimension (VC-dimension) of a feedforward neural net with linear threshold gates is at most $O(w \cdot \log w)$, where $w$ is the total number of weights in the neural net. We show in this paper that this bound is in fact asymptotically optimal. 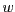More precisely, we exhibit for any depth $d \geq 3$ a large class of feedforward neural nets of depth d with $w$ weights that have VC-dimension $\Omega (w \cdot \log w)$. 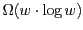This lower bound holds even if the inputs are restricted to Boolean values. The proof of this result relies on a new method that allows us to encode more "program-bits" in the weights of a neural net than previously thought possible.

Reference: W. Maass. Neural nets with superlinear VC-dimension. Neural Computation, 6:877-884, 1994.