The perceptron (also referred to as McCulloch-Pitts neuron, or linear threshold
gate) is commonly used as a simplified model for the discrimination and
learning capability of a biological neuron. Criteria that tell us when a
perceptron can implement (or learn to implement) all possible dichotomies
over a given set of input patterns are well-known, but only for the idealized
case where one assumes that the sign of a synaptic weight can be switched
during learning. We present in this article an analysis of the classification
capability of the biologically more realistic model of a sign-constrained
perceptron, where the signs of synaptic weights remain fixed during learning
(which is the case for most types of biological synapses). In particular, the
VC-dimension of sign-constrained perceptrons is determined, and a necessary
and sufficient criterion is provided that tells us when all
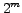
dichotomies
over a given set of m patterns can be learned by sign-constrained perceptron.
We also show that uniformity of L1 norms of input patterns is a sufficient
condition for full representation power in the case where all weights are
required to be nonnegative. Finally, we also exhibit cases where the
sign-constraint of a perceptron drastically reduces its classification
capability. Our theoretical analysis is complemented by computer simulations,
which demonstrate in particular that sparse input patterns improve the
classification capability of sign-constrained perceptrons.