Oracle dependent properties of the lattice of NP-sets

S. Homer and W. Maass

Abstract:

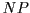
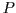
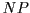
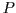
We consider under the assumption $P \neq NP$ questions concerning the structure of the lattice of $NP$ sets together with the sublattice $P$. We show that two questions which are slightly more complex than the known splitting properties of this lattice cannot be settled by arguments which relativize. 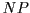The two questions which we consider are whether every infinite $NP$ set contains an infinite $P$ subset and whether there exists an $NP$-simple set. We construct several oracles, all of which make $P \neq NP$, and which in addition make the above-mentioned statements either true or false. 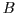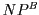In particular we give a positive answer to the question, raised by Bennett and Gill 1981), whether an oracle $B$ exists making $P^B \neq NP^B$ and such that every infinite set in $NP^B$ has an infinite subset in $P^B$. 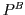The constructions of the oracles are finite injury priority arguments.

Reference: S. Homer and W. Maass. Oracle dependent properties of the lattice of NP-sets. Theoretical Computer Science, 24:279-289, 1983.