Threshold circuits of bounded depth

A. Hajnal, W. Maass, P. Pudlak, M. Szegedy, and G. Turan

Abstract:

We examine a powerful model of parallel computation: polynomial size threshold circuits of bounded depth (the gates compute threshold functions with polynomial weights). Lower bounds are given to separate polynomial size threshold circuits of depth 2 from polynomial size threshold circuits of depth 3 and from probabilistic polynomial size circuits of depth 2. 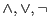With regard to the unreliability of bounded depth circuits, it is shown that the class of functions computed reliably with bounded depth circuits of unreliable $\wedge, \vee ,\neg$ gates is narrow. On the other hand, functions computable by bounded depth, polynomial-size threshold circuits can also be computed by such circuits of unreliable threshold gates. Furthermore we examine to what extent imprecise threshold gates (which behave unpredictably near the threshold value) can compute nontrivial functions in bounded depth and a bound is given for the permissible amount of imprecision. We also discuss threshold quantifiers and prove an undefinability result for graph connectivity.

Reference: A. Hajnal, W. Maass, P. Pudlak, M. Szegedy, and G. Turan. Threshold circuits of bounded depth. Journal of Computer and System Sciences, 46:129-154, 1993.