Meanders and their applications in lower bound arguments

N. Alon and W. Maass

Abstract:

The notion of a meander is introduced and studied. Roughly speaking, a meander is a sequence of integers (drawn from the set $N= \{I, 2, . . . ,n\}$) that wanders back and forth between various subsets of 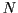$N$ a lot. Using Ramsey theoretic proof techniques we obtain sharp lower bounds on the minimum length of meanders that achieve various levels of wandering. We then apply these bounds to improve existing lower bounds on the length of constant width branching programs for various symmetric functions. 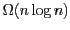In particular, an $\Omega (n \log n)$ lower bound on the length of any such program for the majority function of $n$ bits is proved. We further obtain optimal time-space trade-offs for certain input oblivious branching programs and establish sharp lower bounds on the size of weak superconcentrators of depth 2.

Reference: N. Alon and W. Maass. Meanders and their applications in lower bound arguments. J. Comput. System Sci., 37:118-129, 1988. Invited paper for a special issue of J. Comput. System Sci.