Factor graphs: Robot Localization [5 P]

Implement the sum-product algorithm for factor graphs in MATLAB for the Gaussian Bayesian network illustrated in Fig. 5 with the probabilities given in Eq. 1 - 3.

Figure: Robot control task.

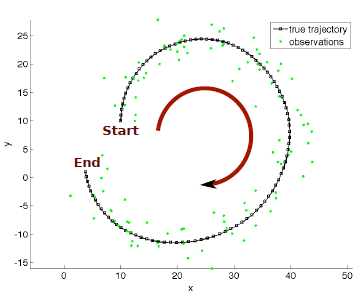
Modify the files mainTemplate.m, kalmanFilter.m and kalmanSmoother.m available for download on the course homepage² and implement a) the Kalman filter algorithm and b) the Kalman smoother algorithm. The task is to infer the trajectory of a robot that starts at position ${\bf x}_0$ and moves according to the linear transition model

$${\bf x}_{t+1} = {\bf A}{\bf x}_{t} + {\bf B}{\bf u}_{t} + \mathcal{N}(0\vert{\bf Q})$$ (5)

for given actions ${\bf a}_t$ from the observations (green dots)

$${\bf y}_{t} = {\bf D}{\bf x}_{t} + {\bf d} + \mathcal{N}(0\vert{\bf C})$$ (6)

as illustrated in Fig. 6. The environment and the parameters for the linear state transition and observation model are already provided in the file mainTemplate.m.

Investigate and discuss the results for both algorithms. Hand in figures of representative results that show the actual robot trajectories and the most likely robot trajectories for both algorithms as infered by the sum-product algorithm.

Present your results clearly, structured and legible. Document them in such a way that anybody can reproduce them effortless. Hand in printouts of your MATLAB code.