Next: Clustering: Face recognition [3
Up: MLA_Exercises_2011
Previous: EM Algorithm Applet [3
Assume that the training examples
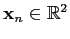 with
with 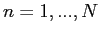 were generated from a mixture of
were generated from a mixture of 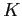 lines
lines
where
and the hidden variable 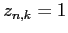 if
if 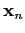 is generated from line
is generated from line 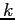 and 0 otherwise.
Derive the update equations for the M-step of the EM algorithm for the variables
and 0 otherwise.
Derive the update equations for the M-step of the EM algorithm for the variables
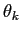 and
and 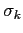 .
.
Haeusler Stefan
2011-12-06
![]() with
with ![]() were generated from a mixture of
were generated from a mixture of ![]() lines
lines